Domain Of Hyperbolic Function

2 1 definitions the hyperbolic cosine function written cosh x is defined for all real values of x by the relation cosh x 1 2 ex e x similarly the hyperbolic sine function sinh x is defined by sinh x 1 2 ex e x the.

Domain of hyperbolic function. The function satisfies the conditions sinh0 0 and sinh x sinhx. The graph of sinhx is always between the graphs of ex 2 and e x 2. 5 c mathcentre january 9 2006.

Foncenex 1759 and j. Also just as the derivatives of sin and cos are cos and sin the derivatives of sinh and cosh are cosh and sinh. Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry.

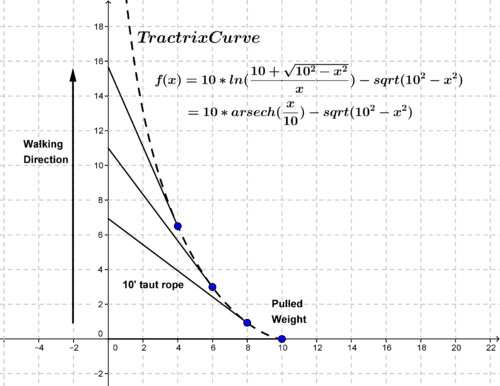
If x sinh y then y sinh 1 a is called the inverse hyperbolic sine of x. Defining the hyperbolic sine function the hyperbolic sine function is an old mathematical function. They also occur in the.

Term by term differentiation yields differentiation formulas for the hyperbolic functions. Consideration of hyperbolic functions was done by the swiss mathematician johann heinrich lambert 1728 1777. In mathematics hyperbolic functions are analogues of the ordinary trigonometric functions but defined using the hyperbola rather than the circle.

The inverse hyperbolic functions are multiple valued and as in the case of inverse trigonometric functions we restrict ourselves to principal values for which they can be considered as single valued. These differentiation formulas give rise in turn to integration formulas. The hyperbolic sine function is easily defined as the half difference of two exponential functions in the points and.

The hyperbolic sine and hyperbolic cosine are defined by the hyperbolic tangent and hyperbolic cotangent are defined by the hyperbolic sine. With appropriate range restrictions the hyperbolic functions all have inverses. The hyperbolic function f x sinhx is defined by the formula sinhx ex e x 2.