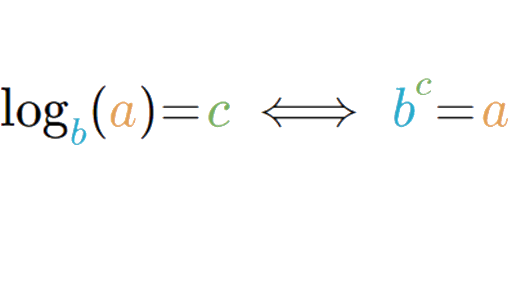Domain Meaning Logarithm

In mathematics the logarithmic function is an inverse function to exponentiation.

Domain meaning logarithm. The base of the logarithm is a. F x log a x. Examples on how to find the domain of logarithmic functions with solutions.

Before working with graphs we will take a look at the domain the set of input values for which the logarithmic function is defined. Domain and range of exponential and logarithmic functions recall that the domain of a function is the set of input or x values for which the function is defined while the range is the set of all the output or y values that the function takes. The domain can also be given explicitly.

When finding the domain of a logarithmic function therefore it is important to remember that the domain consists only of positive real numbers. For x 0 a 0 and a neq 1 y log a x if and only if x a y. In addition we discuss how to evaluate some basic logarithms including the use of the change of base formula.

The complex logarithm is needed to define exponentiation in which the base is a complex number. Parentheses are sometimes added for clarity giving ln x log e x or log x. That is the argument of the logarithmic function must be greater than zero.

In this section we will introduce logarithm functions. One can also replace log a by other logarithms of a to obtain other values of a b differing by factors of the form e 2πinb. Then the function is given by.

The domain of y is latex left infty infty right latex. This can be read it as log base a of x. Recall that the exponential function is defined as latex y b x latex for any real number x and constant latex b 0 latex latex b ne 1 latex where.